[DL] 인공 신경망의 학습 과정(Learning Process of ANN)

2021. 12. 30. 21:36

인공 신경망의 학습 과정(Learning Process of ANN)

(인공 신경망을 모르신다면 이 링크 먼저 보시는게 좋아요! 인공 신경망)

인공 신경망은 어떻게 학습할까?

인공 신경망 학습 과정

위 이미지(속칭 움짤)는 인공 신경망의 학습 과정을 나타낸 것이다.
먼저 움짤이 보여주는 순서대로 인공 신경망의 학습 과정을 말로 풀어보자.

① : 데이터 입력(입력층) -> 가중치-편향 연산 & 활성화 함수 연산 반복 수행(은닉층)
② : ①의 연산 결과(예측값) 출력(출력층)
③ : 예측값과 실제 값의 차이 계산 by 손실 함수
④ : ③의 계산 결과에 따라 가중치 갱신 by 경사 하강법
⑤ : 기준 만족할 때까지 ①~④ 과정 반복
(기준 : 학습 횟수, 성능 평가 점수 등 사용자 지정 요소)

여기서 ①, ②가 이루어지는 과정을 순전파(Forward Propagation),
③은 손실 계산 (또는 그냥 손실 함수 그 자체),
④는 역전파(Backward Propagation)라고 한다.

그리고 ①부터 ④까지 한 번 수행된 것을 두고 iteration 또는 epoch라고 하는데, 이는 학습시키는 데이터의 단위(=배치 사이즈(batch size))에 따라 다르다.
만약 데이터가 잘게 나뉘어서 조각조각 학습되었다면 하나의 조각이 위 과정을 한 번 수행했을 때 이를 1 iteration이라고 한다.
그리고 잘게 나뉘었든 통짜든 전체 데이터 뭉치가 한 번 위 과정을 거쳤다면 이를 1 epoch라고 한다.
자세한 내용은 아래에서 다루겠다.

※ 참고 : iteration과 epoch의 의미

iteration
the process of doing something again and again, usually to improve it, or one of the times you do it

epoch
a long period of time, especially one in which there are new developments and great change

- Cambridge English Dictionary

그럼 구체적으로 인공 신경망의 각 학습 과정에서 무슨 일이 벌어지고 있는지 들여다 보자.

순전파(Forward Propagation; Feed Forward)

순전파와 역전파를 순(順)과 역(逆), 전파(傳播)로 나누어서 보자.
전파(傳播)는 무언가를 널리 전달하여 퍼지게 하는 것이다.
순(順)은 순한 또는 순응한다는 뜻이고 역은 거꾸로, 거스른다는 뜻이다.

그럼 무엇을 전파하는 것인가? 간단하다. 입력받은 값이다.
자, 무언가가 들어왔다. 그럼 나갈 곳도 있어야 하는게 순리이다(월급이 들어오면 기다렸다는 듯이 카드값이 나가듯...).
따라서 순전파는 들어온 값이 나가는 방향으로 자연스럽게 퍼져가는 것이다.
반대로 역전파는 나갈 곳에서 나가지 않고 거꾸로 들어온 방향으로 거슬러 가는 것이다.

인공 신경망에서의 순전파도 똑같은 이치이다.

1) 이전 단계(입력층 또는 이전 은닉층)에서 값이 들어온다.
2) 이에 대해 가중치-편향 연산을 수행한다.
3) 그리고 가중합으로 얻은 값을 활성화 함수를 통해 다음 층으로 전달한다.

손실 함수(Loss Function)

연습생(입력층)부터 시작해 하드 트레이닝(순전파)을 거쳐온 $x_1$(입력값)이 마침내 최종 오디션(출력층)에 도달하였다.
이제 세상에 나를 드러내기만 하면 된...다고 생각하던 찰나, 대표님(손실 함수 J)이 말한다.
"응 아직 아니야, 돌아가~ 돌아가는 길에 스타일이랑 컨셉 싹 고쳐서 다시 트레이닝 해달라고 해~ 너 아직 데뷔 못해~"

손실 함수는 순전파를 통해 출력층에 도달한 값, 즉 신경망의 예측값을 실제 데이터의 타겟 값과 비교하여 그 차이를 계산한다.
차이를 계산하는 방법은 다양한데, Keras 기준으로 자주 사용되는 몇 가지는 다음과 같다.

binary_crossentropy
categorical_crossentropy$^*$$^1$
sparse_categorical_crossentropy$^*$$^1$
그 외 mean_squared_error, mean_absolute_error 등

차이 계산을 마쳤으면 그 차이를 줄이기 위해서 먼 길을 험난하게 거쳐온 출력값들을 가차없이 되돌려보낸다.

그냥 보내는가? 아니다. 왔던 길 되돌아가면서 각 길목 담당자(노드)한테 다음 번에 더 잘 할 수 있게 개선 좀 하라고 하며 돌려보낸다.

역전파(Backward Propagation; Backpropagation)

"트레이너(노래 담당 - 노드)님, 대표님이 저 다시 하래요. 근데 스타일이랑 컨셉 싹 다 고치래요."
"그래? 그럼 창법을 두성으로 바꾸자!"
"트레이너(댄스 담당 - 노드)님, 대표님이 저 다시 하래요. 근데 스타일이랑 컨셉 싹 다 고치래요."
"그래? 그럼 힙합 스타일로 가자!"
"트레이너님", "트레이너님", "트레이너님" ...
... 모든 트레이너와 스타일 및 컨셉 논의를 마치고서 $x_1$은 다시 연습생이 되어야 한다.

자, 손실 함수한테 퇴짜맞고서 이제 왔던 길을 되돌아가려고 한다.
그런데 그냥 터덜터덜 가면 안 되고, 가는 길목 길목 담당자마다 만나서 개선해야 한다 말하고 실제로 개선까지 같이 해야 되돌아갈 수 있다!

역전파는 손실 함수를 통해서 얻은 손실 정보를 출력층부터 입력층까지 전달하여 매 단계 가중치가 어떻게 조정되어야 할지 구하는 과정이다.

그럼 이 가중치는 어떻게 조정을 하는가?
이때 사용되는 방법이 바로 경사 하강법(GD; Gradient Descent)이다.

경사 하강법(GD; Gradient Descent)

"$x_1$. 어디 가니?"
"앗, GD 선배님! 저 대표님에게 퇴짜맞아서 다시 처음으로 되돌아가는 중입니다..."
"그렇군. 다음 번에 또 퇴짜맞으면 안 되잖아, 그렇지?"
"네 맞아요! 근데 저 어떻게 해야할지 모르겠어요..."
"걱정마! 내가 너에게 또 퇴짜맞지 않도록 가이드를 해주지!"
"!!!"

경사 하강법은 역전파 과정에서 손실 함수의 값을 줄이기 위한 방법 중의 하나이다.
우선 손실 함수를 표현한 그래프를 보자.

가로축은 가중치, 세로축은 손실 함수 값이다.
손실 함수의 값을 줄이기 위해서는 맨 아래에 위치한 최소값을 향해서 가야 할텐데, 어떻게 도달할 수 있을까?
간단하다. 손실 함수의 기울기가 작아지는 방향으로 가중치를 갱신하는 것이다.

기울기는 어떻게 구하지?
간단하다. 손실 함수를 미분한 함수, 즉 손실 함수의 도함수가 바로 기울기이다.
따라서 손실 함수의 도함수를 계산하여 이 값이 작아지도록 가중치를 조정한다.

그럼 구체적으로 가중치 갱신 과정을 알아보자.

가중치 갱신 과정

위 이미지는 $i$번째 가중치인 $\theta_i$가 갱신되는 모습을 수식으로 표현한 것이다.
$\eta$는 경사를 얼마나 큰 보폭으로 내려갈지 결정하는 것이고,
$\theta_{i,j}$의 $j$는 iteration을 의미한다.
$J(\theta)$는 가중치 $\theta$에 대한 손실 함수이며,
$\partial$는 편미분 기호이다.

해당 가중치에 대한 손실 함수의 기울기는 손실 함수를 해당 가중치로 편미분한 $\frac{\partial J(\theta)}{\partial \theta_{i, j}}$로 표현된다.

기울기가 작아지는 방향으로 가중치를 움직여야 하므로 기울기 값에 음의 부호(-)를 붙인다. 이러면 양수 기울기는 음수로, 음수 기울기는 양수가 되어 매 갱신마다 가중치가 손실 함수의 최소값에 가까워지도록 만든다.

가중치 조정 결과

역전파 편미분 계산 과정 with 연쇄 법칙(Chain Rule)

위에서 가중치 $\theta_{i, j}$에 대한 손실 함수의 기울기는 $\frac{\partial J(\theta)}{\partial \theta_{i, j}}$인 것을 확인했다. 근데 이건 또 어떻게 구하지?
여기서 편미분과 함께 연쇄 법칙이 사용된다.

먼저 가중치, 이전 입력값, 편향과 현재 입력값, 그리고 출력값의 손실 함수로 이루어진 그래프를 그려보자.

$wx+b$가 활성화 함수 $Z$를 거쳐서 출력값 $y$가 되었고, y는 손실 함수에 전해져 손실 함수값 J가 나왔다.
$\partial w$, $\partial Z$, $\partial y$, $\partial J$는 $w$, $Z$, $y$, $J$ 각각을 미분한 것을 의미한다.

여기서 가중치에 대한 손실 함수의 미분값(기울기)는 $\frac{\partial J}{\partial w}$로 나타낼 수 있는데, 이를 한 번에 계산할 수가 없다.
왜냐하면 $J$와 $w$ 사이에 여러 가지 계산 과정이 자리를 잡고 있기 때문이다. 따라서 중간 보스 격파 후에 최종 보스를 깨듯이 이 각각의 단계를 순차적으로 깨야 한다. 이 과정은 아래와 같이 표현된다.

$$\frac{\partial J}{\partial w} = \frac{\partial J}{\partial y} \cdot \frac{\partial y}{\partial Z} \cdot \frac{\partial Z}{\partial w}$$

이런 식으로 $\partial J$와 $\partial w$의 중간에 위치한 노드도 미분 과정에 포함시켜 이어붙이는 것이다. 이러한 계산 방식을 연쇄 법칙(Chain Rule)이라고 한다.

※ 손실 함수를 왜 J라고 표시할까?

명확한 출처는 찾지 못했으나, 인터넷 상에 올라온 의견들을 보면 오래 전부터 미적분학에서 사용했다거나, 'Jacobian'에서 따왔다거나, Loss에서 L을 거울에 비추듯 뒤집은 것이라는 등의 내용이 있었다.
(확실한 내용을 아시는 분께서는 코멘트 남겨주시면 감사하겠습니다!)

옵티마이저(Optimizer)

"감사합니다, GD 선배님! 덕분에 제 스타일이랑 컨셉도 저에게 딱 맞게 다 바꿨어요! 근데 저뿐만 아니라 저랑 비슷한 처지인 친구들이 산더미인데, 혹시..."
"아, 그러면 나 말고 나보다 빠릿빠릿한 친구가 있거든? 그 친구한테 가봐. 이름은 SGD야."

위에서 경사 하강법을 통해서 손실 함수의 기울기를 계산하여 가중치를 갱신한다는 것을 알았다.
허나 경사 하강법은 모든 입력 데이터에 대해서 손실 함수의 기울기를 계산하기 때문에, 데이터가 커질 경우에는 계산 과정이 상당히 오래 걸리게 된다.
이 문제를 각자 나름의 방법으로 최적화하는 친구들이 있으니, 이 친구들을 묶어서 옵티마이저라고 한다.

단순하게 말하자면, 가파른 경사길을 어떤 방식으로 내려올 것인지 지정하는 것이다.
후딱 빠르게 내려갈지, 천천히 주변을 살필지, 보폭을 크게 혹은 작게 할지 등등.

우선 너무 꼼꼼한 나머지 대량의 데이터에는 굼떠버리는 GD를 대신하여 신속함(달리 말하면 성급함)을 미덕으로 삼는 SGD(Stochastic Gradient Descent)를 먼저 만나보자.

1) 확률적 경사 하강법(SGD; Stochastic Gradient Descent)

"(연습생 그룹) 안녕하세요 SGD 선배님, 잘 부탁드립니다!"
"왔구나? 오케이, 일단 너 하나 먼저 가자!"
"에?"
(잠시 뒤)
"우선 한 번 됐고, 이런 식으로 하나씩 돌아가면서 다들 어떻게 할지 각을 재보자!"
'(연습생 그룹) 뭔가... 불안하다... !'

확률적 경사 하강법은 전체 데이터에서 하나의 데이터만 뽑아서 손실 계산 및 역전파 과정을 수행하는 방식이다.
즉, 한 번의 iteration마다 1개의 데이터만 사용하는 것이다.

데이터를 1개만 쓰다 보니 가중치를 업데이트하는 속도는 매우 빠르다.
문제는 1개만 쓰기 때문에 학습 과정에서 경사 하강이 이리 갔다 저리 갔다 불안불안 불안정한 모습을 보인다.

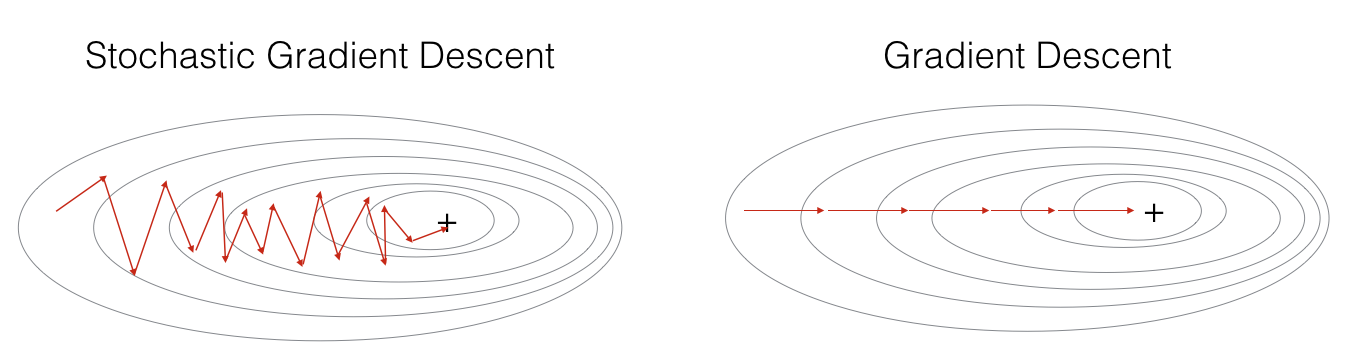
전부 다 투입시키자니 한 세월이 가고,
그렇다고 하나씩 보내서 빨리 빨리 하려니 가는 애들마다 이랬다 저랬다 난리라서 불안하고...
그러면 적당히 작은 그룹으로 나눠서 보내면 전부 다 보내는 것보다는 빠르고, 하나만 보내는 것보다는 덜 왔다 갔다 하지 않을까?

그래서 나온 방법이 미니 배치 경사 하강법(Mini-batch GD)이다.

2) 미니 배치 경사 하강법(Mini-batch GD)

"한 명씩 보내니까 너무 이랬다 저랬다 하네?
그럼 이제부터는 그룹 단위로 가서 맞춰보자!"

전체 데이터를 작게 쪼개어서 학습 과정에 보내는 방식이다.
어느 정도의 크기로 나누는가에 따라 학습 속도나 가중치 갱신의 최적점 도달 등의 결과가 달라진다.
여기서 데이터를 나누어주는 크기를 배치 사이즈(Batch size) 라고 한다.

배치 사이즈(Batch size)
- 미니 배치 경사 하강법에서 사용하는 미니 배치의 크기
- 일반적으로 2의 배수로 설정
- 메모리 용량에 여유가 있다면 가능한 한 큰 배치 사이즈를 쓰는 것이 안정적인 학습 진행에 유리함

배치 사이즈가 작을 때

배치 사이즈가 작아질수록 경사 하강법의 가중치 갱신이 불안정해진다. 이로 인해 최적점 도달에 많은 iteration이 필요해진다.

하지만 동시에 불안정, 즉 노이즈(noise)가 많기 때문에 지역 최적점(Local Minima)에서 빠져나와 전역 최적점(Global Minima)에 도달할 확률이 높아진다는 장점도 있다.

배치 사이즈가 클 때

배치 사이즈가 커질수록 가중치 갱신이 안정적이므로 최적점 도달에 비교적 적은 iteration만 필요해진다.

그러나 배치 사이즈를 너무 크게 설정하면 메모리 용량을 초과해버리는 Out-of-Memory 문제가 발생할 수도 있으므로 적당한 배치 사이즈를 설정해야 한다.

데이터 수와 배치 사이즈, iteration의 관계
$$
\text{# of Data = Batch size} \times \text{Iteration}
$$
순전파부터 역전파까지, 즉 가중치를 한 번 갱신하는 단위가 iteration이다. 그리고 미니 배치 경사 하강법에서는 배치 사이즈 단위로 iteration을 진행한다.

따라서 전체 데이터의 수는 배치 사이즈와 iteration을 곱한 값이라고 할 수 있다.

3) 그 외 옵티마이저들

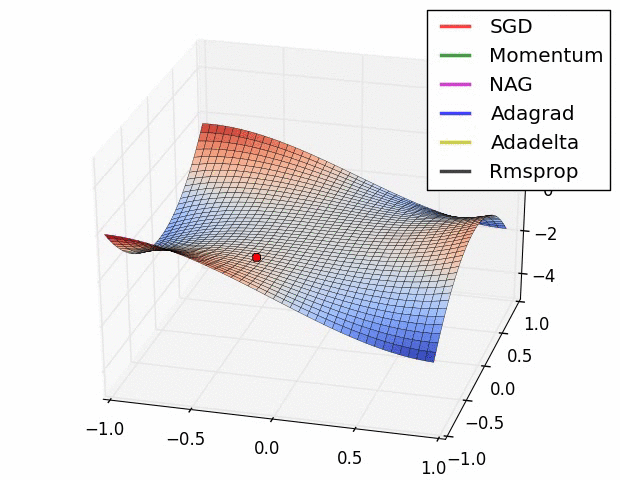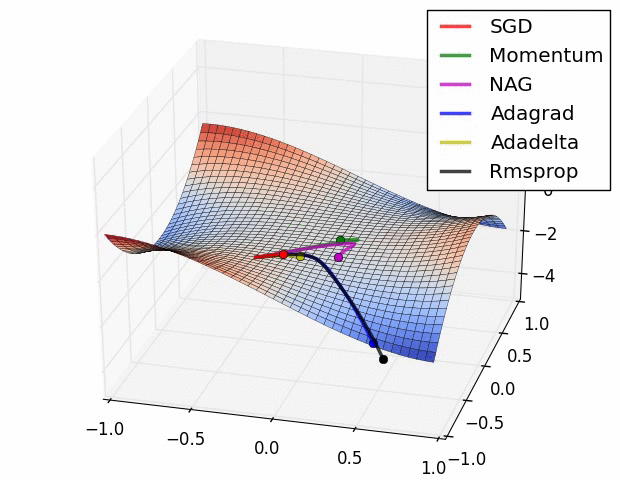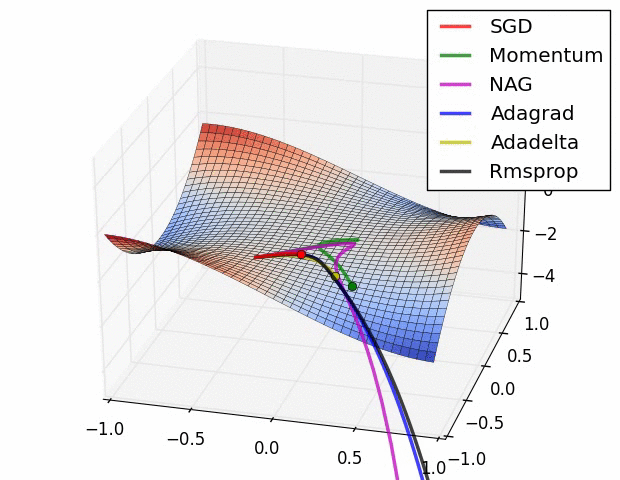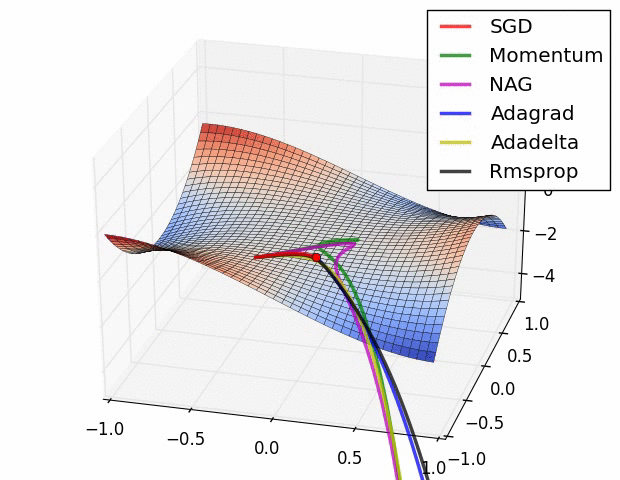
GD와 SGD, Mini-batch GD 이후로 아래와 같이 다양한 옵티마이저들이 나왔다.

각각이 가진 특징을 간단한 비유로 표현해보겠다.

Momentum : 가던 방향으로 더 빨리 잘 가게 밀어주기
AdaGrad : 모르는 곳은 휙휙 둘러보고, 아는 곳은 자세하게 들여다 보기
RMSProp : 매 발걸음마다 내가 가는 이 길이 맞는지 아닌지 점검하며 가기
AdaDelta : AdaGrad의 개선 버전. 자세히 보는건 좋은데 멈추진 말고 계속 가면서 보기
Adam : AdaGrad와 RMSProp의 퓨-전(fusion). AdaGrad처럼 상황에 따라 보폭 조절하고, RMSProp처럼 제대로 가고 있는지 봐가면서 움직이기

이 중에서 Adam이 현재 가장 널리 사용되는 옵티마이저이다.
그렇다고 모든 상황에서 만능은 아니므로, 다루는 데이터의 성질과 해결할 문제 등을 고려하여 옵티마이저를 선택해야 할 것이다.

*1 categorical_crossentropy VS sparse_categorical_crossentropy

categorical_crossentropy와 sparse_categorical_crossentropy 모두 이름에서 알 수 있듯이 분류 문제를 위한 손실 함수로 쓰인다.
그럼 저 sparse가 붙고 안 붙고의 차이는 무엇인가?

우선 TensorFlow API 문서에 나온 예시를 보자.
# categorical_crossentropy
y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
loss = tf.keras.losses.categorical_crossentropy(y_true, y_pred)
assert loss.shape == (2,)
loss.numpy()
array([0.0513, 2.303], dtype=float32)
# sparse_categorical_crossentropy
y_true = [1, 2]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred)
assert loss.shape == (2,)
loss.numpy()
array([0.0513, 2.303], dtype=float32)

위 예시 모두 3개의 클래스가 있고, 실제 타겟값은 1번 클래스와 2번 클래스를 의미한다.
여기서 둘의 표현 방식이 달라진다. categorical_crossentropy는 타겟값이 One-hot Encoding 되어 있는 반면에 sparse_categorical_crossentropy는 정수값이 그대로 있다.

그럼 각각 어떤 때에 사용해야 할까?

우선 sparse_categorical_crossentropy는 하나의 타겟 특성만 있는 경우 사용하면 될 것이다.
한 개의 타겟 특성 내에 여러 개의 클래스가 있는 경우이다.
예) Fashion MNIST

categorical_crossentropy는 타겟 특성이 One-hot Encoding되어 여러 개로 나누어졌거나 타겟 값이 여러 특성에 동시에 속할 수 있는 혹은 타겟 값이 여러 특성에 걸친 확률값인 경우 사용하는게 좋을 것이다.
예) One-hot Encoding : [1,0,0], [0,1,0], [0,0,1]
여러 특성에 걸친 경우 : [0.5, 0.3, 0.2]

<참고 자료>

저작자표시

'Deep Learning > ANN' 카테고리의 다른 글

[DL] 활성화 함수(Activation Function) (0)	2021.12.23
[DL - Tensorflow/Keras] 인공 신경망(ANN; Artificial Neural Network) (0)	2021.12.22

세상, 나 그리고 개발